好玩的网站列表

1. 树

• 父节点
  • 上层的节点
• 兄弟节点
  • 父节点是同一个节点
• 叶节点
  • 没有子节点的节点
• 高度
  • 节点到叶子节点的最长路径
• 深度
  • 根节点到这个节点所经历的边的个数
• 层
  • 节点的深度 + 1

2. 二叉树

每个节点最多有两个分叉的树，即最多有两个子节点

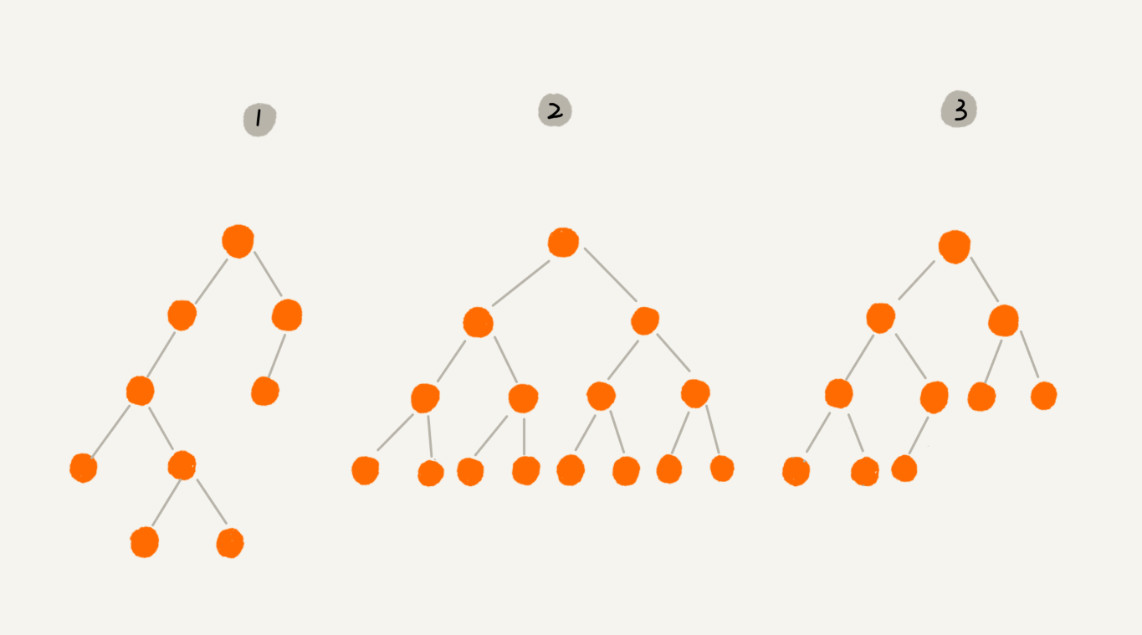
2 显示的是满二叉树，特点是叶子节点都在最底层，出了叶子节点之外，每个节点都有左右两个子节点

3 叶子节点都在最底下两层，并且出了最后一层，其他的层的节点数量都要达到最大，并且最后一层的节点都是靠左排列的，这种二叉树叫做完全二叉树。

2.1 如何表示/ 存储一棵二叉树？

2.1.1 基于指针或者引用的二叉链式存储法

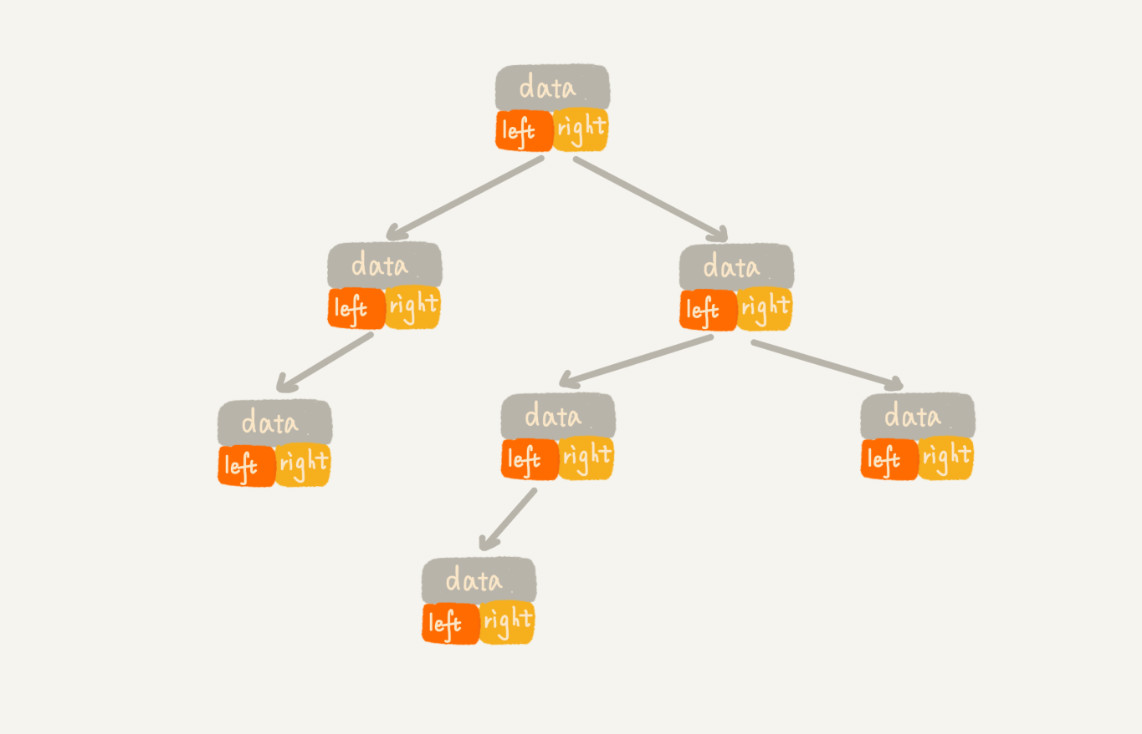
每个节点都有三个字段，其中一个存储数据，另外两个指向左右子节点的指针。因此通过根节点，我们就可以通过左右子节点的指针将整棵树都串起来了。

2.1.2 基于数组的顺序存储法

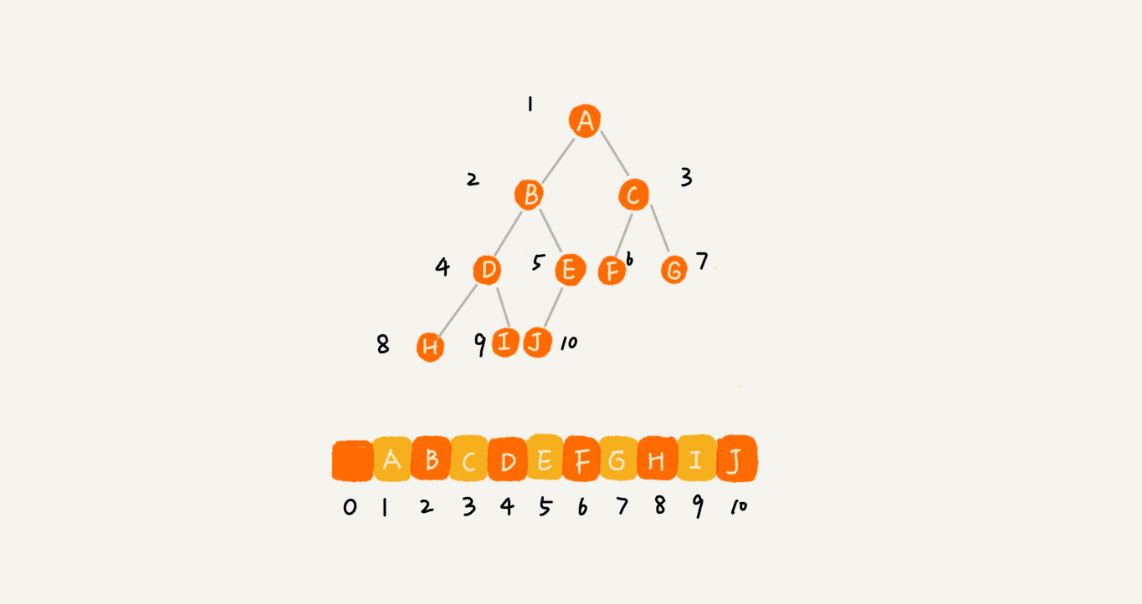
如果节点X存储在数组中下标为i的位置，下标为2i的位置存储的是左子节点，下标为2i + 1的位置存储的就是右子节点。下标为i/2的位置存储的就是它的父节点了。通过这种方式，我们只要知道根节点存储的位置，就可以通过下标计算，把整棵树都串起来。 不过对于一棵非完全二叉树而言，会浪费比较多的数组存储空间的。

2.2 二叉树的遍历

2.2.0 递归公式

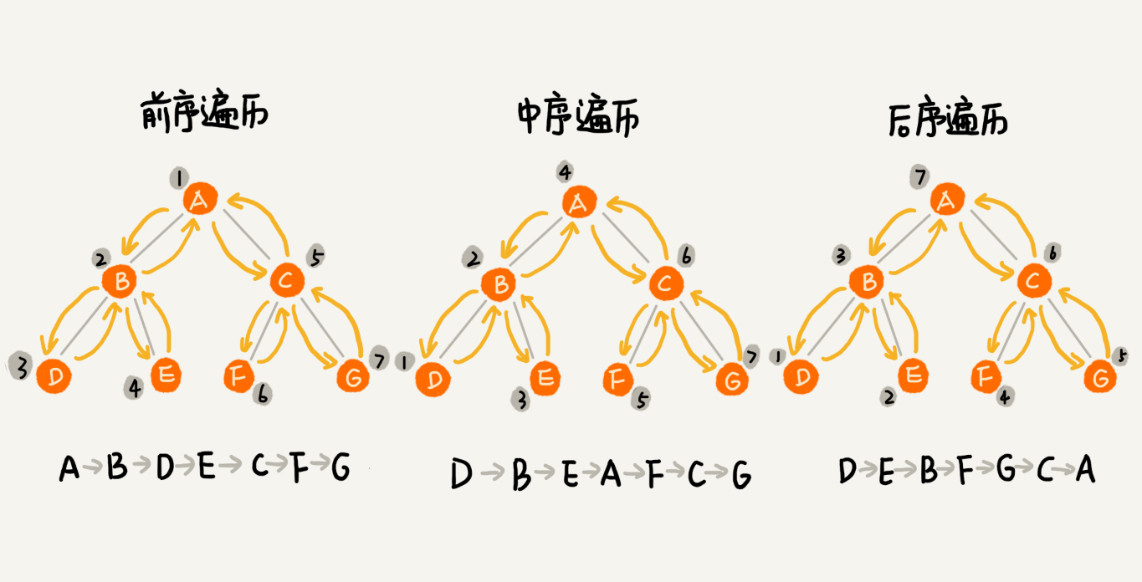
二叉树的遍历整体就是一个递归的过程

写递归代码的关键，就是看能不能写出一个递推公式。而递推公式的关键，就是如果要解决问题A，就假设子问题B,C都已经解决，然后再来看如何利用B，C来解决A

前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

// 前序遍历
void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印root节点
  preOrder(root->left);
  preOrder(root->right);
}

// 中序遍历
void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印root节点
  inOrder(root->right);
}

// 后序遍历
void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印root节点
}

2.2.1 前序遍历

对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。

2.2.2 中序遍历

对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树

2.2.3 后序遍历

对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身

3. 二叉查找树

支持动态数据集合的快速插入、删除、查找操作。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 stone2paul@gmail.com